NFA 转 DFA

NFA

$$\delta(p, 0) = \{ q \} \\ \delta(p, 1) = \Theta \\ \delta(q, 0) = \{ q \} \\ \delta(q, 1) = \{ q, r \} \\ \delta(r, 0) = \Theta \\ \delta(r, 1) = \Theta \\$$

DFA

$$\delta((q, r), 0) = \{ q \} \\ \delta((q, r), 1) = \{ q, r \} \\$$

$\epsilon$ NFA 转 无 $\epsilon$ NFA

$\epsilon$-闭包：每个状态的 $\epsilon$-闭包定义为此状态 仅接受空串能够到达的状态的集合（包括该状态自身）。

$$\delta(q, a) = \epsilon\;闭包(\delta(q, a))$$

由 DFA 构造正则表达式

状态消去法：消去状态，让转移条件是正则表达式。

DFA 的化简

状态等价：两个状态接受相同的串能在最后达到同一终止状态， 则两状态等价。

填表法

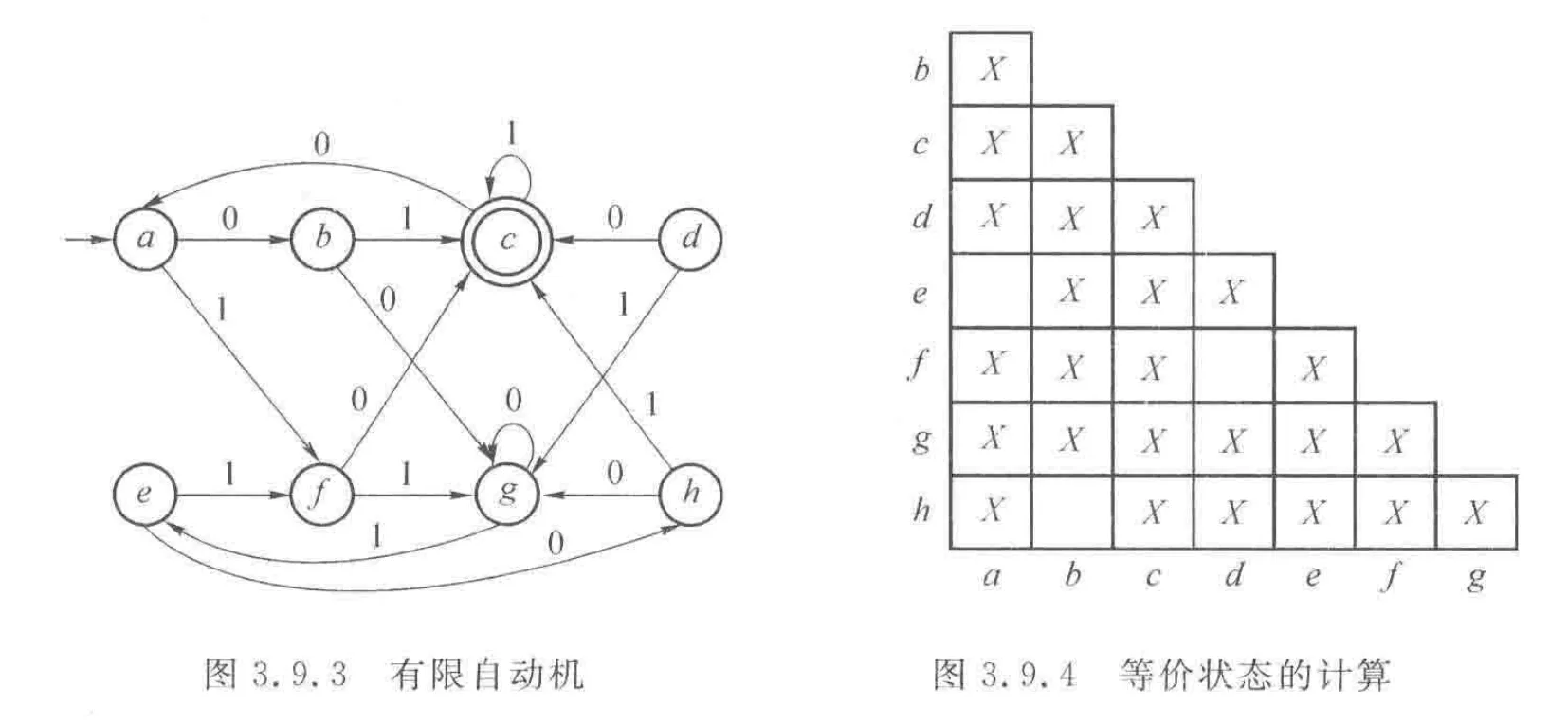
1. 按照非终结符和终结符画出第一批不等价状态

2. 如果两个状态能通过相同的输入到达两个不等价状态， 则这两个状态也不等价

3. 重复第 2 步，最后剩下的几组即为等价状态，将每组分别写为 新的状态，如：[a, b]

有输出的有限自动机

米兰机

“输出在边上“

摩尔机

“输出在状态节点上”

从摩尔机构造等价米兰机

“把输出从节点按照箭头反方向写到边上”

泵引理

定理：设 $L$ 是正则集，存在常数 $n$， 对字符串 $\omega \isin L$ 且 $|\omega| \geq n$， 则 $\omega$ 可以写成 $\omega_0\omega_1\omega_2$， 其中 $|\omega_1\omega_0| \leq n$, $|\omega_0| > 0$， 且对所有的 $i \geq 0$ 有 $\omega_1\omega_0^i\omega_2 \isin L$。

用泵引理证明某个语言不是正则语言

证明方法：反证法。假设这个语言是正则语言，使用泵浦引理。 如果发现了某个i使循环体循环i次之后得到的串不满足语言要求， 则这个语言不是正则语言 （因为正则语言循环体循环任意次都满足要求）。

---